𝜆xyz.xy(zx)
𝜆x.𝜆y.𝜆z.xy(zx)
[x := zx]𝜆y.𝜆z.xy
𝜆y.𝜆z.zxxy
𝜆xyz.xy(zxy)
𝜆x.𝜆y.𝜆z.xy(zxy)
[x := zxy]𝜆y.𝜆z.xy
𝜆y.𝜆z.zxyxy
𝜆xy.xy(zxy)
𝜆x.𝜆y.xy(zxy)
[x := zxy]𝜆y.xy
𝜆y.zxyy
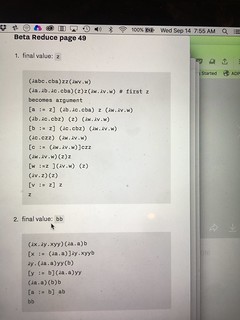
(𝜆abc.cba)zz(𝜆wv.w)
(𝜆a.𝜆b.𝜆c.cba)(z)z(𝜆w.𝜆v.w) # first z becomes argument
[a := z] (𝜆b.𝜆c.cba) z (𝜆w.𝜆v.w)
(𝜆b.𝜆c.cbz) (z) (𝜆w.𝜆v.w)
[b := z] (𝜆c.cbz) (𝜆w.𝜆v.w)
(𝜆c.czz) (𝜆w.𝜆v.w)
[c := (𝜆w.𝜆v.w)]czz
(𝜆w.𝜆v.w)(z)z
[w :=z ](𝜆v.w) (z)
(𝜆v.z)(z)
[v := z] z
z
(𝜆x.𝜆y.xyy)(𝜆a.a)b
[x := (𝜆a.a)]𝜆y.xyyb
𝜆y.(𝜆a.a)yy(b)
[y := b](𝜆a.a)yy
(𝜆a.a)(b)b
[a := b] ab
bb
(𝜆y.y)(𝜆x.xx)(𝜆z.zq)
[y := (𝜆x.xx)]y(𝜆z.zq)
(𝜆x.xx)(𝜆z.zq)
[x := (𝜆z.zq)]xx
(𝜆z.zq)(𝜆z.zq)
[z := (𝜆z.zq)]zq
(𝜆z.zq)(q)
[z := q]zq
qq
(𝜆z.z)(𝜆a.aa)(𝜆b.bc)
[z := (𝜆a.aa)]z(𝜆b.bc)
(𝜆a.aa)(𝜆b.bc)
[a := (𝜆b.bc)]aa
(𝜆b.bc)(𝜆b.bc)
[b := (𝜆b.bc)]bc
(𝜆b.bc)(c)
[b := c]bc
cc
(𝜆x.𝜆y.xyy)(𝜆y.y)y
[x := (𝜆y.y)]𝜆y.xyy(y)
(𝜆y.(𝜆y.y)yy)(y)
[y := y](𝜆y.y)y(y)
(𝜆y.y)(y)y)
[y := y] (y)(y)
yy
(𝜆a.aa)(𝜆b.ba)c
[a := (𝜆b.ba)]aac
(𝜆b.ba)(𝜆b.ba)c
[b := (𝜆b.ba)]bac
(𝜆b.ba)a(c)
[b := a]bac
aac
(𝜆xyz.xz(yz))(𝜆x.z)(𝜆x.a)
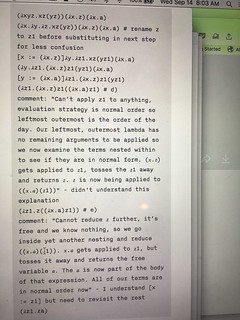
(𝜆x.𝜆y.𝜆z.xz(yz))(𝜆x.z)(𝜆x.a) # rename z to z1 before substituting in next step for less confusion
[x := (𝜆x.z)]𝜆y.𝜆z1.xz(yz1)(𝜆x.a)
(𝜆y.𝜆z1.(𝜆x.z)z1(yz1)(𝜆x.a)
[y := (𝜆x.a)]𝜆z1.(𝜆x.z)z1(yz1)
(𝜆z1.(𝜆x.z)z1((𝜆x.a)z1) # d)
comment: "Can’t apply z1 to anything, evaluation strategy is normal order so leftmost outermost is the order of the day. Our leftmost, outermost lambda has no remaining arguments to be applied so we now examine the terms nested within to see if they are in normal form. (𝑥.𝑧) gets applied to 𝑧1, tosses the 𝑧1 away and returns 𝑧. 𝑧 is now being applied to ((𝑥.𝑎)(𝑧1))" - didn't understand this explanation
(𝜆z1.z((𝜆x.a)z1)) # e)
comment: "Cannot reduce 𝑧 further, it’s free and we know nothing, so we go inside yet another nesting and reduce ((𝑥.𝑎)(𝑧1)). 𝑥.𝑎 gets applied to 𝑧1, but tosses it away and returns the free variable 𝑎. The 𝑎 is now part of the body of that expression. All of our terms are in normal order now" - I understand [x := z1] but need to revisit the rest
(𝜆z1.za)